9a. Failure Theories  (SSES Ch. 9.0-9.2)
• Types of Failure • Max. Normal Stresses
• Max. Shear Stress • Max. Distortional Energy 		Back | Index | Next
Types of Failure

There are two basic types of material failure:

  • Fracture - or brittle failure - occurs when a material breaks in two after only a small amount, if any, plastic deformation. Ceramics (e.g., silicon carbide), concrete and glass are examples of materials that exhibit brittle failure.
  • Yielding - or ductile failure - occurs when a material undergoes permanent (plastic) deformation. Metals such as aluminum, steel and copper are examples of materials that exhibit such failure.

A state of plane stress has three non-zero stress values: sx, sy, and txy. While we can assess when a material fails when subjected to a uniaxial stress (sx-only), or for shear-stress-only (txy) - see Chapt.3- we do not yet have a good model to determine when a material point fails under a general state of stress (sx, sy, and txy).

Three failure theories are now introduced:

  • Maximum Normal Stress Failure Theory (brittle materials)
  • Maximum Shear Stress Failure Theory (ductile materials)
  • von Mises Failure Theory (ductile materials)
Maximum Normal Stress

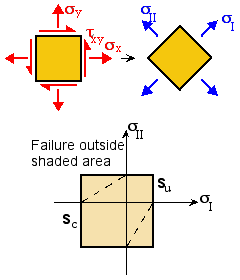
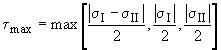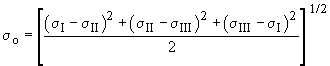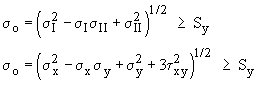The Maximum Normal Stress criterion states that when the maximum normal stress in any direction of a brittle material reaches the strength of the material - the material fails. Thus, finding the Principal Stresses at critical locations is important.

Failure occurs when:

sI > Su or sII > Su
   (tension)
|sI| > |Sc| or |sII| > |Sc|
  (compression)
  • Su is the ultimate strength in tension
  • Sc is the ultimate strength in compression
  • Sc > Su for brittle materials; a typical ratio is Sc ~ 10Su
The above plot is a Failure Map. If the Principal Stresses fall outside of the shaded area, failure occurs.
Tresca - Maximum Shear Stress
   - for Plane Stress only

The Tresca Yield states that a ductile materials yields (fails) when the Maximum Shear Stress exceeds the shear strength ty the material yields.

The Maximum In-Plane Shear Stress is the average of the in-plane Principal Stresses.

The TWO Maximum Out-of-Plane Shear Stresses are:

Note that the Out-of-Plane Principal Stress (sIII) for the plane stress condition is zero.

Failure occurs when the maximum of the three Maximum Shear Stresses

reaches the shear yield stress, ty.

The above plot is a Failure Map.
If the in-plane Principal Stresses lie outside of the shaded zone, failure occurs.

  • Under a uniaxial load, sII = sIII = 0. Thus, the axial yield stress is sI = SY = 2ty. The Maximum Shear Stress Theory predicts that the Shear Yield Stress is half the Axial Yield Stress.
  • When the In-Plane Principal Stresses are the same sign (1st and 3rd quadrant), the Maximum Shear Stress in the system is Out-of-Plane.
    When the In-Plane Principal Stresses are opposite sign (2nd and 4th quadrant), the Maximum Shear Stress in the system is In-Plane.
von Mises - Maximum Distortion Energy

The von Mises Yield Criterion states that a ductile material fails (yields) when the von Mises Stress so exceeds the yield strength Sy.

The von Mises Stress (or Equivalent Stress) is defined by:

When so = Sy the material is deemed to have yielded.

For plane stress (sz = txz = tyz = 0) the von Mises Failure Criterion reduces to:

Using the general relationship with sx = sy = 0, the von Mises criterion predicts that ratio of the axial yield strength to the shear yield strength is: Sy = 1.732ty.

From the Tresca condition the predicted relationship between the yield strength and shear yield strength is: Sy = 2ty.

In general, metals tend to follow the axial yield strength-shear yield strength relationship of von Mises, making von Mises more accurate. However, von Mises is slightly harder to use, and any system that falls within the Tresca boundary, also falls within the von Mises boundary.

 

von Mises Failure Surface

The above plot is a Failure Map. If the In-plane Principal Stresses lie outside the shaded zone, failure occurs. The dashed lines indicate the Tresca failure surface.
Top Back | Index | Next
Updated: 05/23/09 DJD