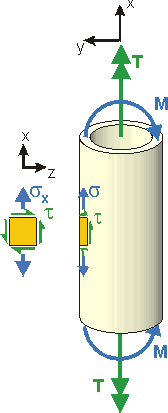
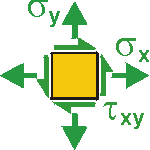
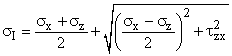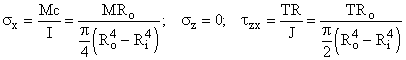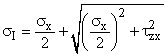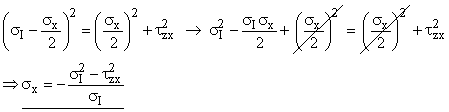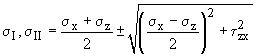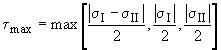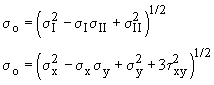Background: The shaft of a femur (thigh bone) can be approximated as a hollow cylinder. The significant loads that it carries are torques and bending moments.

Given: The femur shaft has an outside diameter of 24 mm and an inside diameter of 16 mm. The tensile strength of bone is taken to be S_u = 120 MPa.
During strenuous activity, the femur is subjected to a torque of 100 N·m.

Req'd: The effective moment the bone can take without failure. Consider only torsion and bending loads, and take the bone to be a brittle material.

Sol'n: Since the bone is brittle, it follows the Maximum Normal Stress criteria. If the maximum Principal Stress is greater than the material Tensile Strength, s_I > S_u, the bone fails (fractures).

The element is taken on the left side of the femur as we look at it; the element is in the z-x plane. The Maximum Principal Stress is:

Solving the geometric terms:

so:    t = TR_o/J = 45.9 MPa

Reducing the s_I equation:

and rearranging:

For the bone to break, s_I = S_u = 120 MPa.
Since t = 45.9 MPa, we can solve for s_x : s_x = 102.44 MPa.

Using the Bending Stress formula (s=Mc/I), the Moment to break the bone is:

Given: A plane stress element in a part made of the 6061-T6 is found to have the following stress:
        s_x = 5.6 ksi; s_y  = 9.9 ksi;  t_xy = 5.0 ksi
The axial yield strengthof 6061-T6 aluminum is 35 ksi, and its shear yield stress is t_y = 20 ksi.

Req'd: Determine the Factor of Safety:
  (a) using the Tresca Criterion.
  (b) using von Mises Criterion.

Sol'n:

Step 1. The Tresca Criterion is based on the maximum shear stress. The in-plane principal stresses are:

Solving:   sI = 13.2 ksi        sII = 2.3 ksi

Considering all directions, for plane stress, the maximum shear stress is:

The maximum shear stress is out-of-plane, t_max = 6.6 ksi

Step 2. The von Mises Criterion is based on a maximum distortion energy. The von Mises ( Equivalent) Stress for a plane-stress element is:

If the Equivalent Stress s_o exceeds the yield stress, the material is deemed to have yielded.

Using either equation, solving for the equivalent stress gives: s_o = 12.2 ksi

• The ratio S_y:t_y for design values of 6061-T6 Aluminum is 35:20 = 1.75.
• From the von-Mises Criterion, S_y:t_y=1.732.
• From Tresca,t_y = S_y/2 = 17.5 ksi, or S_y:t_y=2.
• Thus, the von Mises Model is the better model for 6061-T6 Aluminum.