8a. Stress Transformation  (SSES Ch. 8.0-8.3)
• Rotation of a Stress Element • Principal Stresses
• Maximum In-Plane Shear Stress 		Back | Index | Next
Why Stress Transformation  

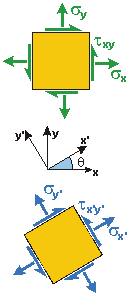
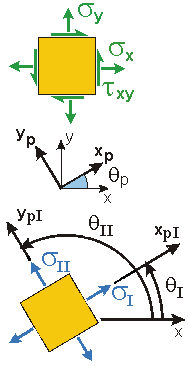
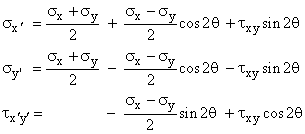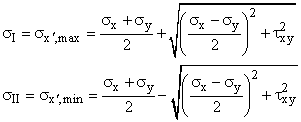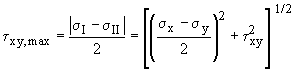So far, we have looked at stress elements (material points under stress) that align with a typical x-y-z coordinate system. The x-y-z coordinate system are convenient when calculating stresses from the applied loads.

However, there are times when rotating or transforming the stress element to view it in another direction is necessary. Two reasons to view a stress element in another orientation include:
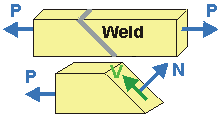
  • To determine the stress in another direction (e.g., normal and parallel to the the plane of a weld);
  • To determine the Maximum Normal Stress or the Maximum Shear Stress at a point (useful to assess if a material in a complex state of stress will fail).
Rotation of a Stress Element

Stress on a rotated element are derived using trigonometry and applying the equilibrium equations. If a plane-stress element is rotated by angle q, the Transformed Stresses are:

  • Angle q is positive in the counter-clockwise direction.
  • Adding the two normal stresses together: sx + sy = sx' + sy
    The sum of the normal stresses is always the same, or invariant.
Principal Stresses

Principal stresses are the maximum and minimum normal stresses (most positive/most negative stresses or most tensile/most compressive stresses) that occur at a point as the set of axes is rotated by angle q. The Principal Stresses are called sI and sII, and occur along the xp-yp axes. The Principal Stresses for a given stress state are:

The larger of the two stresses is generally called sI.

The Principal Stresses occur when the stress element has been rotated by angle qp, where:

This equation has two results: angles, qpI and qpII(90° apart) (or just qI and qII). It is not always obvious which angle goes with which Principal Stress. It is often best to substitute one of principal angles into the general stress-transformation equation for sx'(qp). By doing so, the appropriate angle is matched with the right stress, i.e., sI with qI.

KEY POINT: When the Normal Stresses are Principal Stresses the Shear Stress is Zero. This can be shown by plugging in either of the principal angles into the general equation fortx'y'(qp).
Maximum In-Plane Shear Stress

The maximum (in-plane) shear stress occurs when the principal stress element is rotated by 45°, and is given by:

The angle that defines the direction nomral to the plane on which the Maximum Shear Stress occurs is:

This equation has two solutions, qsI and qsII, one corresponding to a positive shear stress on the newxs-face, and the other to a negative shear stress on the new xs-face (defined by qs). It is often best to substitute one of the angles into the general stress-transformation equation for tx'y'(qs). By doing so, the appropriate angle is matched with the correct shear stress (positive or negative).

Note that qs =qp±45°.

KEY POINT: When Shear Stress is maximum, the Normal Stresses are the same and equal to their average. This can be shown by plugging in either of the Shear Stress Angles into the general equation for sx'(qs) or sy'(qs) .
Top Back | Index | Next
Updated: 05/23/09 DJD