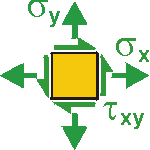
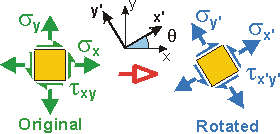
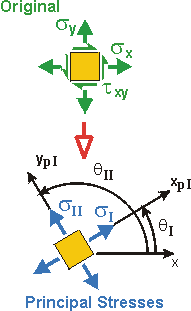
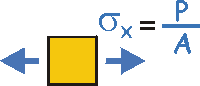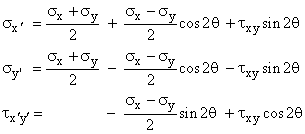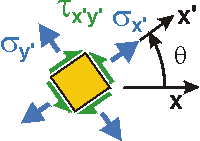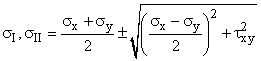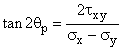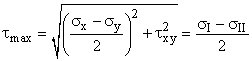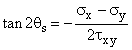Given: A welded plate supports a force of P = 50 kN. The width of the plate W = 200 mm, and the thickness, t = 50 mm. The weld is at 30° from the vertical.
Req'd: Determine the Normal Stress and Average Shear Stress in the weld.
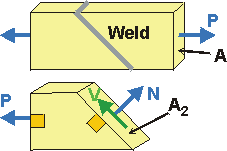
Step 1. The axial stress in the plate is: