Strain Transformation

Strain Transformation at a point (in plane strain) is done in a similar manner as with the stresses. Simply substitute e_x for s_x and e_y for s_y. However, because of the way the math works out, substitute g/2 for t:

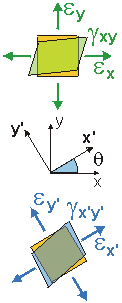
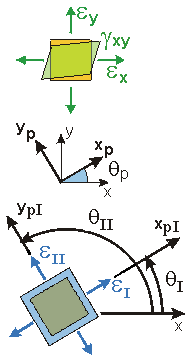
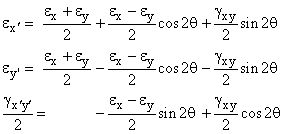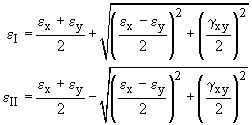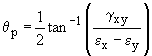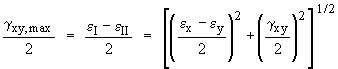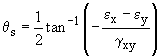Principal Strains

Principal Strains are the maximum and minimum normal strains that occur at a point as the coordinate system is rotated by a certain angle q_p. The principal strains are e_I and e_II, and occur along the x_p-y_p axes. These directions are NOT necessarily the same as those for the Principal Stresses for the associated stress-state.

The Principal Strains for a given strain state are given by:

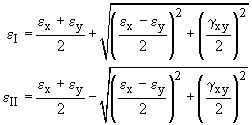
The principal strains occur when the element has been rotated by an angle of q_p, where:

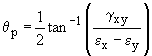
As with the angles for principal stresses, there are two solutions, 90° apart.

KEY POINT: When the Normal Strains are Principal Strains the Shear Strain is Zero.

Maximum (In-Plane) Shear Strain

The Maximum (In-Plane) Shear Strain occurs when the Principal Strain element is rotated 45° and is given by:

The angle at which the Maximum Shear Strain occurs is given by:

Again, there are two solutions, 90° apart.

KEY POINT: When the Shear Strain is Maximum, the Normal Strains are equal to each other and are the average of the Principal Strains.