6c. Beam Deflection  (SSES Ch. 6.2)
• Deflection • Governing Equations • Boundary Conditions		 Back | Index | Next
Deflection
External loads cause beams to deflect transverse to its main axis. The shape of the deflected beam is defined by v(x); v(x) is the deflection of the neutral axis with respect to its original condition. The deflected shape is called the elastic curve. The elastic curve is always:
  • Smooth. The slope equations must be the equal at a junction of any two segments of a beam, regardless of the direction from which the common point is approached.
  • Continuous. The displacement equations must be equal at a junction of any two segments of a beam, regardless of the direction from which the common point is approached.
Governing Equations

Based on the moment-curvature relationship, the governing differential equation for the deflection of an elastic beam, for small deflections:

EI is called the bending stiffness or flexural rigidity of a beam. v''(x) is the curvature of the beam at position x.


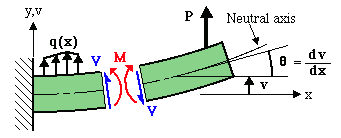
Mouse-over image to see description

Expressions for slope v'(x) and beam deflection v(x) are determined by integrating twice:

Curvature
Slope
Deflection

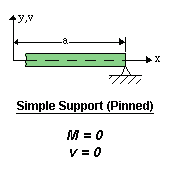
Constants C1 and C2 are determined by considering the beam's geometric boundary conditions.
Boundary Conditions
Boundary Conditions are the constraints imposed on a beams by its supports. In order to solve beam-deflection problems, in addition to the differential beam equations, the boundary conditions must be prescribed at each support. Common boundary conditions are shown at right.
Click on description below to see example.
  • Clamped or fixed support (built-in). The right end of the beam has a clamped support. Displacement ( v ) and slope ( v' ) must both be zero.
  • Simple Support (pin or roller). The right end of the beam has a simple support. Displacement ( v ) must be zero. The beam is free to rotate (the pin does not resist rotation), so the moment (M) must also be zero.
  • Free End. The right end of the beam is a free end. Therefore the beam is free of moment ( M ) and shear ( V )
  • Guided support. The right end of the beam has a guided support and is free to deflect normal to the beam, but is unable to rotate, thus the slope ( v' ) must be zero. Also the support is not capable of resisting shear ( V ).

Click on description at left to see example)
Top Back | Index | Next
Updated: 05/24/09 DJD