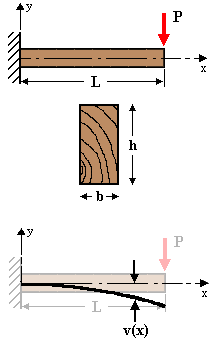
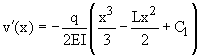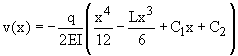Given: A cantilever beam, is built in at the left end, has length L, and rectangular cross-section of width b, and height h. The beam is loaded by point load P at its free end.

Req'd: Determine the deflection at the end of the beam.

Sol'n: The bending moment in the beam is given by:

Therefore the differential equation for bending is:

Integrating with respect to x gives:

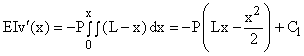
Since the slope at the built-in end is zero, then

Integrating again gives:

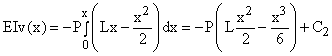
The deflection at the built-in end is zero, so:

Therefore, the equation of the elastic curve - the deflection - is:

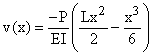
Deflection at the tip is then:

Since the sign of v(L) is negative, the deflection is downward.

Given: A simply supported solid circular beam with radius r = 1.2 in. and length L = 50 in. is subjected to a uniform distributed load of q(x) = 24 lb/in. The beam is made from 6061 aluminum.

Req'd: Determine the maximum deflection of the beam.

Sol'n: Recall from Example Problem 6b.2 that the bending moment and the moment of inertia of the beam are given by:

          

The moment is constant over the entire length of the beam. The curvature of the beam's deflection is then:

Integrating once gives the equation defining the slope of beam:

The constant C₁ will be found later using the boundary conditions.

Integrating a second time gives the deflection of the beam:

The constants C₁ and C₂ are determined using the boundary conditions (BC) . Since the beam is simply supported:

• v(0) = 0
• v(0) = L

Due to symmetry of the load and geometry (supports), another BC that be applied in this case is v'(L/2) = 0.

Solving for the constants:

The deflection of the beam is then::

From the symmetry of the beam we know the maximum deflection is at x = L/2 = 25 in. From the Materials Property Table, E for 6061 aluminum is 10 Msi. The maximum deflection is then: