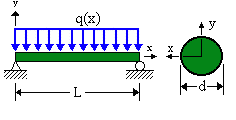
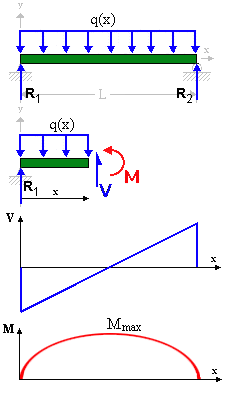
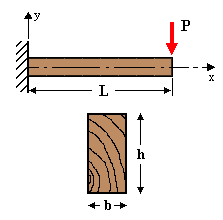
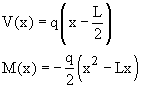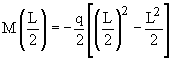Given: A cantilever beam, is built in at the left end, has length L, and rectangular cross-section of width b, and height h. The beam is loaded by point load P at its free end.

Req'd: Determine the moment of inertia I, and maximum bending stress s_x in the beam.

Sol'n: For a rectangular beam with width b, and height h, the Moment of Inertia for bending about the z-axis is:

The moment with maximum magnitude occurs at x = 0:
M_max = –PL. The maximum bending tensile stress occurs at the top surface, y = h/2:

Given: A simply supported solid circular rod with radius r = 1.2 in. and length L = 50 in. is subjected to a uniform distributed load of q(x) = 24 lb/in.

Req'd: Determine:
(a) the maximum moment M_max in the rod.
(b) the moment of inertia I_z of the rod.
(c) the maximum bending stress s_max in the rod.

Sol'n: (a) By summing the forces in the y-direction, the resultant forces can be shown to be R₁ = R₂ = qL/2.

Taking a cut in the rod at an any distance x from the end and treating the length x as a FBD, the shear force and moment in the beam can be determined:

The maximum moment occurs where V(x) = 0, or by symmetry, at x = L/2:

(b) The moment of inertia about the z-axis of the circular cross-section is:

(c) The maximum bending stress is: