| |
|
|
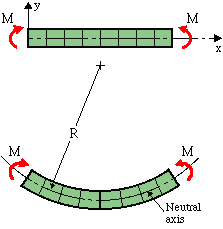
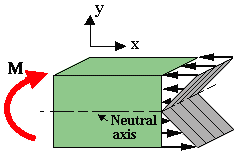
Note the convention:
- A shear force is termed POSITIVE if in acts on a positive face in a positive direction (or on a negative face in a negative direction). A positive shear force on the right-face - the positive x-face - acts upward, in the positive y-direction.
- A positive moment causes a beam to bend into a "happy face"-shape. A moment is POSITIVE if it acts on a positive face about a positive axis (or a negative face about a negative axis). Here, the moment on the right face acts on the +x-face, about the +z-axis, which is out of the plane (screen, paper).
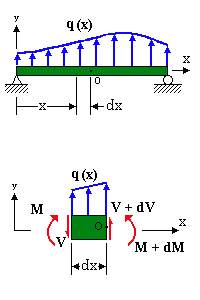
q(x) should be w(x)
and constant over dx.