5a. Torsion Members: Circular Cross-sections
     (SSES Ch. 5.1-5.3, 5.5)
• Thin-Walled Shafts • Solid/Thick-Walled Shafts
• Discretely and Continually Varying Shafts • Power Transmission 		Back | Index | Next
Thin-Walled Torsion Member
In Ch. 3, we introduced the thin-walled circular torsion member at right. The shaft is of length L, average radius R, and thickness t (t<<R), and is subjected to torque, T. Here, the left end (A) of the shaft is fixed, and the right end (B) rotates by angle q, called the angle of twist .

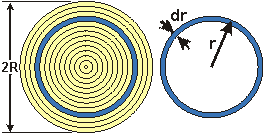
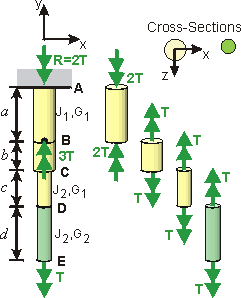
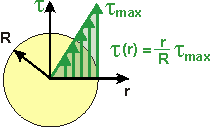If the torque, cross-section and material are all constant over the length, then the following relationships hold for shear strain and shear stress:

Combining the above equations with Hooke's law:

t = Gg

give the angle of twist:

J is the Polar Moment of Inertia.

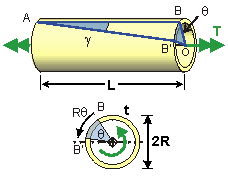
Thin-walled circular shaft

Solid and Thick-walled Torsion Members
Solid and thick-walled shafts can be considered as made up of many thin-walled cylinders of thickness dr, one inside the other. Shear strain and shear stress are a function of the radial position r:

and

Combining gives:

The maximum shear stress is:

J is the Polar Moment of Inertia



Variation of shear stress
in solid circular shaft.
Discretely and Continually Varying Shafts
To solve for the total angle of twist in discretely varying shafts problems - where T, J and G change at discrete points along the axis of the shaft - break the shaft into segments (lengths) over which all the values of T, J and G are all constant. The total angle of twist is the sum of the angle of twist of each sub-length:

Similarly, for problems involving continually varying shafts, the angle of twist can be determined by integrating over the length of the member:

Discretely varying torsion member.
Power Transmission
Power is often transmitted through rotating shafts. The power transmitted by a shaft is given by the torque multiplied by the shaft's angular velocity w:

P = T w
S.I. units:  
U.S. units:  
  • h.p. = Power in horsepower (1 h.p. = 550 ft-lb/sec)
  • r.p.m. = revolutions per minute
Top Back | Index | Next
Updated: 05/24/09 DJD