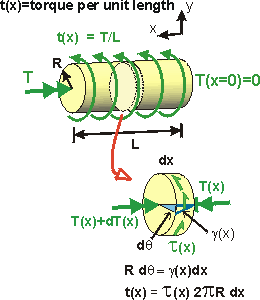
Given: A stepped-shaft (polar moment of inertias J₁, J₂) made of two materials (shear moduli G₁, G₂). The shaft is fixed (no rotation) at the top. Torques are applied about the shaft's axis: 3T (counterclockwise about the +y-axis at Pt. B) and T (clockwise about the +y-axis at Pt. E).

Req'd: Determine the total angle of twist of the bar, q_total.

Sol'n:
Step 1. Equilibrium. Solve for the reaction at Pt. A: R = 2T (clockwise about +y-axis, a negative torque).

Step 2. Twist/Torque of each Segment.
Break up the bar into segments over which all the values (torque, cross-section and modulus) are constant.

The top segment, AB, has length, a, Polar Moment of Inertia, J₁, modulus, G₁, and supports torque 2T (a negative torque on the positive face of AB).

With Cross-section A fixed, the rotation of Section B with respect to fixed Section A is:

Taking each of the other segments with constant torque, section and modulus:

Step 3. Compatibility. The total angle of twist:

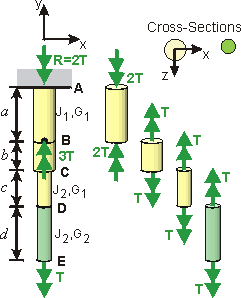
Free Body Diagrams
of shaft segments.

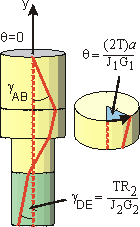
Angular deflection of stepped-shaft.

Given: A drill bit is imbedded a length, L, into a piece of wood. The drill applies a torque of T. The surrounding wood applies a uniform shear force per unit length of the bit acting on the surface of the bit. Assume that the drill bit is a simple cylinder of radius, R and length, L.

Req'd: Determine the angle of twist of the imbedded length. Measure x from where in internal torque is zero, T=0, i.e., from the tip of the bit.

Sol'n:

Step 1. Equilibrium. Over dx, the torque, area and modulus are constant. The torque at cross-section x is T(x) = –T(x/L), where x is measured from the tip of the drill bit.

Step 2. Twist/Torque of Elements. The rotation dq of each dx is:

Step 3. Compatibility. Integrate dq to get the total rotation.

• J(x) = pR⁴/2 and G(x)=G are constant over L.
• Torque T(x) varies from 0 to T, linearly:

T(x)= –(Tx/L)

Drilling into a piece of wood.

 Element dx long extracted from shaft.

Because a negative torque acts on the positive x-face:

T(x) = –T (x/L)

The total rotation is found by integrating:

The negative sign means that, as viewed along the positive x-axis, the left end rotates clockwise w.r.t. the right end. Viewed in the negative x-direction, the rotation of the right end w.r.t. the left is counterclockwise (positive rotation on a negative face).

Given: A drill requires 1/2 hp to turn a 3/8" drill bit at 800 rpm into a block of wood.

Req'd: The maximum shear stress in the drill bit. Model the bit as a solid shaft.

Sol'n:

Step 1. Torque. The maximum torque in the bit occurs at the end closest the drill and is given by:

T = 39.4 lb-in.

Step 2. Shear stress. The maximum shear stress for a solid shaft is: