4a. Axial Members  (SSES Ch. 4.1,4.2)
• Uniform Bar • Discretely Varying Bar • Continually Varying Bar
• Displacement Method

 Back | Index | Next
Uniform Axial Member
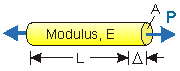
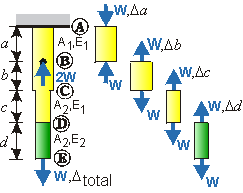
Chapter 3 introduced an axial member of length L subjected to a constant tensile force P acting through the centroid of the bars constant cross-sectional area A. The material modulus E was uniform over the entire length. Since P, A and E are constant over the length of the bar:

Combining these equations gives the change in length of the bar:  

The spring stiffness of an axial member of constant P, A and E over length L is: K = EA/L (P = KD).
Discretely Varying Axial Member
To solve problems involving discretely (suddenly) varying loads, areas, or modulus, the stress and strain at any cross-section at position x are:

To determine the overall change in length, break up the bar into segments of length Li over which the values of force, area and modulus are all constant. Thus:


Discretely varying axial member, broken up into 4 segments over which P, A and E are all constant.

Continuously Varying Axial Member
The load, cross-sectional area and/or modulus in an axial member can vary continuously over the length of an axial member. Reasons for such variations can include:
  • surface friction forces (e.g., dirt acting on a foundation pile, a composite matrix acting on a fiber).
  • body forces (e.g., the self-weight of a column).
  • varying cross-sectional area (e.g., a tapered concrete foundation or a tapered rod).

The length over which P(x), A(x) and E(x) are all constant is differential length dx.

The stress and strain at any cross-section x are:

The total elongation can be determined by integrating over the entire length of the member:

Displacement Method
To solve a system of axial members that is indeterminate - where the forces cannot be solved by statics alone - it is often useful to apply the displacement method. The main steps:
  • Compatibility. Define the displacements (Di) of each member in terms of the overall movement of the system d . The individual members of the system must elongate or move with respect to each other is such a way that they remain together.
  • Hooke's Law. Solve for stresses (s) in each member as a function of displacements (D).length (L), and Young's modulus (E):
    s = Ee = E(D/L)
  • Equilibrium. The sum of the internal forces equals the sum of the applied forces:
    SFinternal = SFapplied;    sA = P
Top Back | Index | Next
Updated: 05/16/2009 DJD