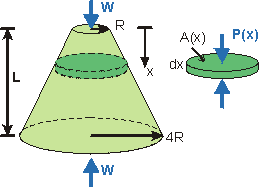
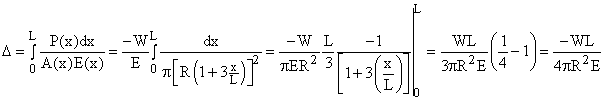Given: A stepped-bar (areas A₁, A₂) made of two materials (moduli E₁, E₂), acted on by forces 2W (upward at Pt. B) and W (downward at Pt. E).

Req'd: Determine the elongation of the bar D_total.

Sol'n:

Step 1. Equilibrium. Solve for internal forces between points where P(x), A(x) or E(x) change.

P_AB = –W;  P_BC = P_CD = P_DE = W

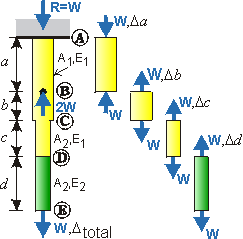
Bar broken up into lengths with
constant force, area and modulus.

Step 2. Elongation/Force Relationship. To solve for the elongation, break the bar into lengths (segments) over which all the values (force, area and modulus) are constant.

The top such segment, AB, has length a, area A₁, modulus E₁, and internal force P_AB = –W (compression). The change in length of AB is:

Since AB is in compression, it shortens: Da<0. Therefore, Point B moves up. Taking each of the other lengths with constant force, area and modulus:

Here, segments BC, CD and DE are all in tension, so each get longer.

Step 3. Compatibility. The total elongation or deflection D_total is:

The displacement of any point (upward or downward) depends on the extension (compression) of the bar segments above it.

Given: A truncated conical pillar supports a weight W.

Req'd: Determine the shortening of the column due to the load. Neglect the weight of the column. Measure x from the top of the pillar.

Sol'n: Break up the column into lengths where the P, A and E are all constant.

Here, it is differential length dx. Over dx, the force, area and modulus are essentially constant. By finding the elongation dD of each dx,

and adding them up - integrating - we find the deflection of the bar.

• P(x) = –W (compression) and E(x)=E are constant over L.
• Area A(x) varies from pR² at the top to p(4R)² at the bottom. We must find an equation for A(x)=p[R(x)]², which is done at the right.

The length with constant force, area and modulus is dx. The stress at any point is s(x) = P(x)/A(x).

    Radius as a function of x:

• At the endpoints:
  • R(x=0) = R;
  • R(L) = 4R.
    
• R increases linearly from R to 4R:

R(x) = R[1+3x/L].

Knowing A(x), sum all of the dD over length L:

The elongation is negative - the column shortens. The effective stiffness for the truncated cone acted on by constant force throughout its length is K_eff = |W/D| = (4pR²E)/L

Given: A stepped bar constrained on both ends is subjected to force P at Point C. Due to the force, Point C moves to the right.

Req'd: Use the displacement method to determine (a) the force P, and (b) the stiffness of the bar K, in terms of the displacement d, Young's modulus E, and the geometric parameters of the bar (area and length).

Sol'n: Solve this problem using the three steps spelled out for the displacement method.

Step 1. Compatibility. The geometric constraint of the system requires that the total change in length of the system be zero:

D_AC + D_CB = 0

or:

Step 2. Hooke's Law. The forces in the two members can be related to the displacements as follows:

Step 3. Equilibrium. Equilibrium requires that:   P + F_AC = F_CB

Combining the three equations gives:

The stiffness of this system is: