4b. Pressure Vessels  (SSES Ch. 4.4)
• Cylindrical Pressure Vessels • Spherical Pressure Vessels
• Deformation of Pressure Vessels   		Back | Index | Next
Pressure Vessels
Pressure vessels contain gasses or liquids under pressure. There are two general shapes: cylindrical and spherical. Due to the internal pressure, the pressure vessels walls are in tension. Pressure vessels can be considered to be thin-walled if the wall thickness is much less than the vessel's radius, e.g., t < 0.1R (or R > 10t). This assumption is generally a good one.
Cylindrical Pressure Vessels
Some examples of cylindrical pressure vessels include propane tanks, fire extinguishers, shaken soda cans, and boilers. Cylindrical pressure vessels are subjected to two stresses: hoop (circumferential) stress sH , and axial (longitudinal) stress sL. Both of these normal stresses are derived by taking cuts through the cylinder and noting that the forces that act across that cut must sum to zero:

Hoop Stress:  F = 0     2pRL = 2sHtL

Hoop Stress FBD.

Longitudinal Stress:  F = 0     ppR2 = sL(2pRt)

Longitudinal Stress on a cross-section.
Spherical Pressure Vessels
Due to the 3D symmetry of thin-walled spherical pressure vessels, stress is uniform (the same) throughout. The spherical stress sS is determined by cutting the sphere in half and applying equilibrium:

F = 0     ppR2 = sS(2pRt)




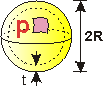
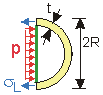Spherical Stress FBD.
Deformation of Pressure Vessels
The deformation of cylindrical and spherical pressure vessels can be determined using Hooke's Law. Because of the biaxial stress state, the Poisson Effect must be considered.
Pressure Vessel
Stress/Strain Elements
Strains
(the reader should be able to derive these)
DR, DL
Cylinder
Sphere
Top Back | Index | Next
Updated: 05/24/2009 DJD