3a. Normal (Axial) Strain and Stress  (SSES Ch. 3.1)
• Normal Strain • Normal Stress • s-e Curve • Young's Modulus
• Poisson's Ratio • Elastic Strain Energy • Fatigue
 Back | Index | Next
Normal Strain

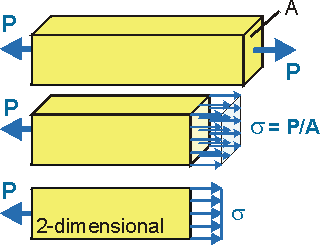
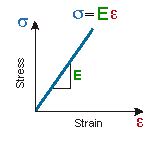
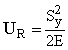When a bar of length L and cross-sectional area A is subjected to axial tensile force P through the cross-section's centroid, the bar elongates D. The change in length divided by the initial length is the bar's engineering strain - or simply strain. The symbol for strain is e (epsilon). The strain in an axially loaded bar is:
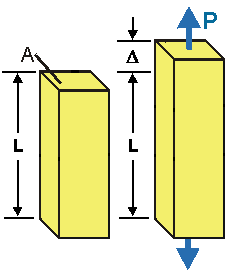
  • Strain is positive in tension (D>0 means e>0) and negative in compression (D<0, e<0).
  • Strain is a fractional change in length - it is dimensionless.
  • Because strain is much smaller than 1, it is typically given as a percentage: e.g., e = 0.003 = 0.3%.

Normal Stress
Consider a bar subjected to axial force P, with a cut taken perpendicular to its axis, exposing the internal cross-section of area A. The force per unit area acting normal to the cross-section is the stress. The symbol used for normal stress - the stress perpendicular to the material surface - is s (sigma). The stress in an axially loaded bar is:
  • Stress is positive in tension (P>0 means s>0), and negative in compression (P<0).
  • English units: psi (pounds per square inch), or ksi (kilopounds per square inch).
  • S.I. units: Pa (Pascal, N/m2), or usually MPa (megapascal, 1 MPa = 1,000,000 Pa).
Stiffness; Young's Modulus
Stiffness is a material's ability to resist deformation. The stiffness of a material is defined through Hooke's Law:

s = E e

where E is Young's Modulus (the modulus of elasticity), a material property. Values of E for different materials are obtained experimentally from stress-strain curves. Young's Modulus is the slope of the linear-elastic region of the stress-strain curve.
  • Young's Moduli for various materials are given in Table 1 - Elastic Constants.
  • E is generally large and given in either ksi (kilopounds per sq.inch) or Msi (megapounds per sq. inch = thousands of ksi), or in GPa (gigapascal).
Stress-Strain Curve
The most common way of depicting the relationship between stress and strain is through a stress-strain curve. Stress-strain curves are obtained experimentally and provide useful material properties such as Young's modulus, yield strength, ultimate tensile strength and failure strain.
Click here to see an animated
Stress-Strain Curve.
  • proportional limit: the value of stress when the stress-strain curve no longer follows Hooke's Law.
  • yield strength, Sy: the practical value of the proportional limit; found using the 0.2% offset rule.
  • ultimate tensile strength, Su: the maximum value of stress that a material can support.
Poisson's Ratio
As you stretch a rubber band, not only does it elongate, but it gets thinner. This is also true for structural components, although it is difficult to see with the naked eye. This response is the Poisson Effect. Poisson's ratio is the negative ratio of the transverse strain (eT) to the longitudinal strain (e), where the longitudinal strain - or direct strain - is the strain in the applied load direction due only to the load.

Poisson's ratio is a materials property. Typical values of Poisson's ratio for various materials are given in Table 1 - Elastic Constants.

Elastic Strain Energy Density
The elastic strain energy density - the elastic strain energy per unit volume - stored in an axial member is:

The maximum value of the elastic strain energy is the resilience, which occurs when the stress in the axial member reaches the yield strength (thus the system is no longer elastic):

Fatigue
The standard fatigue test (zero mean stress) has a strain-time history graph as shown at right. Tests are performed at different stress amplitudes sa = smax , and the number of cycles to failure Nf is recorded. The points (Nf., sa) are plotted and a line fitted. Variables Sf' and b are determined from the curve fit.

The fatigue strength of a material - the value of the stress amplitude for a given value of Nf - can then be calculated:


Stress-time curve.


S-N Curve
Top Back | Index | Next
Updated: 05/10/2009 DJD