Given: A pipe of initial radius R = 0.200 m carries a pressurized liquid that causes the circumferential strain in the pipe to be 0.1% (i.e., the circumference increases by 0.1%).

Req'd: Determine the change in radius of the pipe DR.

Sol'n: Strain e is the change in length divided by the original length. The circumferential strain is 0.1% (0.001). Take L as the circumference of the pipe, and L+D as the circumference under pressure.

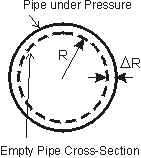
e = [(L+D)-L]/L = [2p(R+DR) - 2pR] / [2pR] = DR/R = 1/1000 = 0.001

The radius increases by: DR = R/1000 = (0.2 m)/1000

DR = 0.0002 m = 0.2 mm

Given: A lamp weighing W = 10 lb hangs from the ceiling by a steel wire of diameter, D = 0.050 inches.

Req'd: Determine is the stress in the wire.

Sol'n: Stress, s, is the force divided by the area. By statics, the force in the wire is: P = W.  

Thus:    s = P/A = P/(pD²/4) = (10 lb)/[p(0.05 in.)²/4]

s = 5093 lb/in² = 5100 psi = 5.1 ksi

Given: The wire holding up the lamp in the above problem has a yield strength (failure strength) of 60 ksi. The Factor of Safety for the design of the wire is to be 1.5 against yielding.

Req'd: Determine the maximum force (the Allowable Force) that the wire can support without exceeding the Allowable (Design) Stress.

Sol'n: The Factor of Safety is: F.S. = [Failure Strength]/[Allowable Stress]. Thus:

s_allow = S_y/F.S. = (60 ksi)/1.5 = 40 ksi

P_allow = s_allowA = 78.5 lb = 78 lb

Note: Do not round up allowables: 79 lb exceeds allowable.