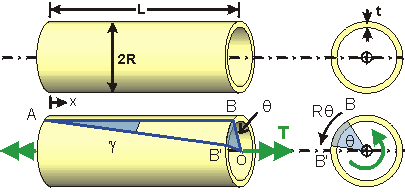
The displacement (of Point B) per unit length of the shaft is the shear strain g (gamma). The displacement of Point B is Rq - perpendicular to the shaft's axis - and so the shear strain is:
| |
| 3b. Shear Stress and Strain (SSES Ch. 3.2) • Shear Strain • Shear Deformation • General Shear Strain • Shear Stress • Complementary Shear Stress • Shear Modulus • Elastic Shear Strain Energy Density |
Back | Index | Next |
|
Shear Deformation
|
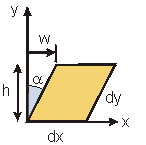
| General Shear Strain |
 |
|
Shear strain g is measured in radians, which is a non-unit (shear strain is dimensionless). |
||
Shear Stress
Shear stress has units of force per unit area (ksi, MPa, etc.). |
The cross-sectional area of a |
|
|
||
|
Complementary Shear Stress
Now consider an element with shear stresses acting on the left and right faces (these faces are on the cross-sections of the last cylinder). To prevent rotation of element, there must be an equal and opposite resisting couple caused by shear stresses at the top and bottom faces of the stress element. These shear stresses are the complementary shear stresses.
|
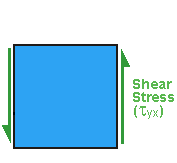
Click here to see the Complementary Shear Stress |
|
Shear Modulus
For isotropic, homogeneous materials only, i.e., steel, aluminum, etc. This is NOT true for composites and other non-isotropic or non-homogeneous materials such as fiber-glass, steel-reinforced concrete, etc. For most metals, n ~ 1/3, which means the G can be approximated:
|
Elastic Shear Strain Energy Density
The maximum value of the elastic strain energy is the shear resilience. It occurs when the stress in the stress reaches the shear yield strength:
|
| Top | Back | Index | Next |