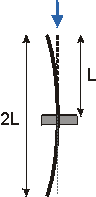
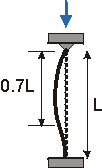
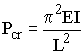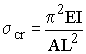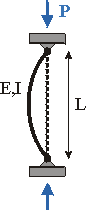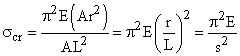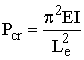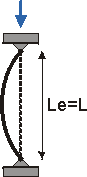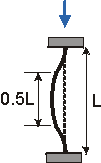When a slender member is subjected to an axial compressive load, it may fail by a condition called buckling. Buckling is not a failure of the material itself (as is yielding and fracture), but is due to geometric instability of the system.
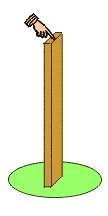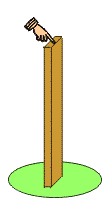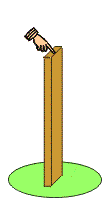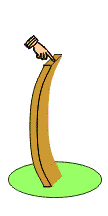 Buckling animation.
Buckling animation.