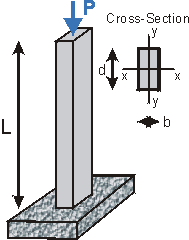
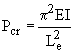Given: An aluminum (E = 70 GPa) column built into the ground has length, L = 2.2 m, and is under axial compressive load P. The dimensions of the cross-section are b = 210 mm and d = 280 mm.

Req'd:
(a) Determine the critical load to buckle the column.
(b) If the yield strength of the aluminum is 240 MPa, is the column more likely to buckle or to yield?
(c) If the factor of safety is F.S.=1.95, what is the allowable buckling load.

Sol'n:
Step 1. The Euler Buckling Formula is:

where L_e is the effective length of the column. The column is fixed-free for buckling about both x- and y-directions. For a fixed-free column, the effective length is:

L_e = 2L = 4.4 m

The column may buckle about the x- or y- axis. The moment of inertia for a rectangle is:

The effective length of
a fixed-free column
is L_e =2L

Here:   I_x = 3.84 x 10⁸mm⁴ and I_y = 2.16 x10⁸ mm⁴

The smaller moment of inertia governs since it results in the smaller Euler Buckling load.
This load is:

Step 2. Will the column Buckle or Yield?

The Buckling Strength is the Euler Buckling Load divided by the area A=bd:  

• If s_cr < S_y = 240 MPa, the column will buckle (as compressive stress s increases from zero, the buckling strength is reached first);
• If s_cr > S_y, the column will yield (s reaches S_y first).

In this our case, the column will buckle.

Step 3. Allowable Load P_allow against buckling with a factor of safety of F.S. = 1.95.

The factor of safety is:  F.S. = (Failure Load)/(Allowable Load):

P_allow = P_cr / F.S. = (7711 kN)/(1.95)