10b. Buckling Considerations  (SSES Ch. 10.4)
• Transition Zone • Bracing • Bifurcation  		Back | Index | Next
Transition Zone

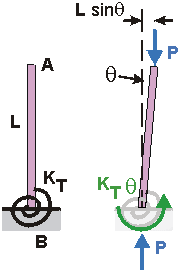
For long columns (large slenderness ratio s), the Euler Buckling Strength reduces rapidly. For very short columns (small s) the Buckling Strength is large. However, the column's strength cannot exceed the material's compressive strength Sc. Depending on the slenderness ratio, a column fails by either:

  • Material Failure (e.g., yielding in metals), or
  • Geometric Instability (buckling)

A transition point between yielding and buckling can be determined by setting the buckling strength equal to the yield strength: scr = Sy. The Transition Slenderness Ratio is then:

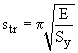
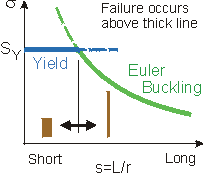
Critical Stress vs.
Slenderness Ratio
In reality, a sudden change from one failure mechanism to another does not happen. Columns of Intermediate Length are governed by equations which provide a transition between yielding and buckling. Steel, aluminum and wood each have unique transitional equations in design manuals for their particular industry.

Bracing

Columns can be braced to increase their buckling strength by reducing the unsupported length of the column. The images below illustrate the effects of bracing a column:

Braced Columns of industrial building. The center column is of I-beam shape, and is braced to resist buckling/bending about its weak axis.
Model of column under axial compressive load, with I-beam cross-section. The column is pinned at top and bottom, and braced at its midpoint.
Buckling about Strong Axis. I-beams have a greater moment of inertia about their strong axis and thus can have longer unbraced lengths about that axis.
Buckling about Weak Axis. Bracing reduces the effective length. Here, it is reduced by 2, increasing the buckling strength by 4.
Pictures from the class web-page of Kirk Martini.

Bifurcation

Consider the rigid post AB of length L, supported at B by a torsional spring of stiffness KT. Axial load P is applied at A. Suppose the post has a slight angular displacement q. The moment caused by the load helps to tip AB; the spring resists the angular motion. Equilibrium gives:

S M = 0 = KTq – P(Lsinq)

For small q, sinq ~ q, so the result reduces to:


Rigid post AB supported by torsional spring under force P.

Thus:

  • if q = 0 the column remains perfectly upright (even if P > KT/L), until failure due to the material being unable to the load support load.
  • if P < KT/L the column remains perfectly upright.
  • if P = KT/L the column remains standing, at angle q.
  • if P > KT/L the column tips over.
Top Back | Index | Next
Updated: 05/22/09 DJD