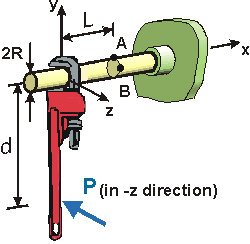
Given: A force of P = 40 lb is applied (along the –z-axis) to the handle of a pipe wrench to tighten a solid shaft into its socket. Let, d = 15 in., R = 1.0 in., and L = 20 in.
Req'd: Determine the normal stress, sx at Point B (x=L, y=0, z=R).
| Practice Problem 7-5 (a) | Back | Index | Next |
|
Given: A force of P = 40 lb is applied (along the –z-axis) to the handle of a pipe wrench to tighten a solid shaft into its socket. Let, d = 15 in., R = 1.0 in., and L = 20 in. Req'd: Determine the normal stress, sx at Point B (x=L, y=0, z=R). |

|
Consider Point B:
- the is no axial force, so no axial stress occurs at B.
- bending moment My, causes a tensile bending stress at B.
- the other stresses that act in the x-y-z coordinate system are shear stresses.
The normal stress at B is only caused by the bending moment::
sx = MyR/I
The moment of inertia for a solid circle is I = pR4/4, so:
sx = 4PL/[pR3] = 4(40 lb)(20 in.)/[p(0.5 in.)3] = 1020 psi
sx = 1020 psi
| Top | Back | Index | Next |