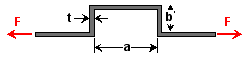
Given: The square aluminum (E = 10 Msi) bar at right is subjected to a tensile force of F = 100 lb. Let t = 1 in., a = 24 in. and b = 5 in.
Req'd: Determine the maximum normal stress in the bar.
| Practice Problem 7-2 | Back | Index | Next |
|
Given: The square aluminum (E = 10 Msi) bar at right is subjected to a tensile force of F = 100 lb. Let t = 1 in., a = 24 in. and b = 5 in. Req'd: Determine the maximum normal stress in the bar. |

|
The axial stress in this section the force divided by the cross-sectional area:
sA = F/t2
The maximum bending stress is sB = Mc/I, which for a square beam is:
sB = 6M/t3
Here, the bending stress is compressive at the top, and tensile at the bottom. Combining the axial stress and the tensile bending stress gives:
smax = F/t2 + 6Fb/t3
smax = 100 lb/(1 in.)2 + 6(100 lb)(5 in.)/(1 in.)3 = 3100 psi
smax = 3.1 ksi
| Top | Back | Index | Next |