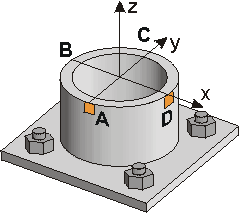
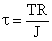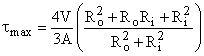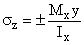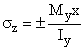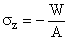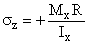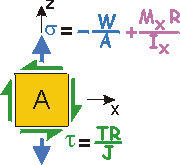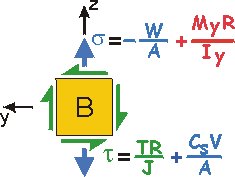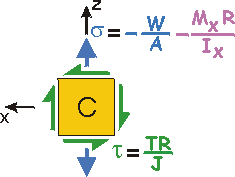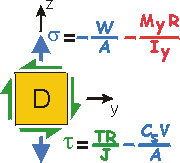Given: Consider the road sign of Example 2b.5. The forces, moments, and torque acting at a cross-section near the base of the mast are shown and right (Cut A-A).

Req'd: Determine the stress states at the surface of the mast, at Points A, B, C and D. Point :
        • A is on the windward side (facing the wind),
        • C is on the "leeward side" (back side),
        • B is on the left side, and
        • D is on the right side of the mast.
Draw 2-d stress elements as you look from the outside of the mast inward.

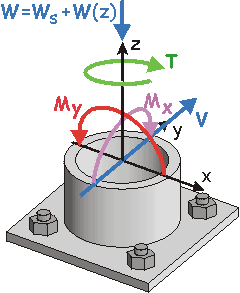
Forces, Moments and Torque acting at Cut A-A.

Road Sign

Sol'n:
Step 1. Consider the five different types of loads acting at the cross-section individually. Then, determine the stresses that each load causes, and at what points the stresses act.

Each load causes the mast to act as a different type of member, e.g.:

• Under the torque, the mast acts as a torsion member.
• Because of the shear force, the mast acts as a beam.
• The weight makes it act like an axial member.

Step 2. Consider how each of the loads affects Point A.

Loads Causing Stresses at Point A.   Coordinates:   x=0, y= –R
Load	Mast Acts as	Stress Equation for Stress at Surface.	Does Pt. A "feel" this stress?	Stress that acts at Point A
Torque, T	Shaft about z-axis		Yes – entire cross-section supports torque
Shear Force, V	Beam about x-axis		No – shear stress is zero at the "top and bottom" of a beam (Points A&C) - the mast acts as a beam bending against the shear force caused by the wind	0
Moment, Mx	Beam about x-axis		Yes (tension) – bending stress is maximum at "top and bottom" of beam
Moment, My	Beam about y-axis		No – bending stress is zero at Centroidal Axis, about which beam is bending (the y-axis for My)	0
Axial Force, W=Ws+Wm(z)	Axial Member		Yes (compression) – entire cross-section supports axial load

Point A feels three stresses:

1. shear stress due to the torque;
2. normal stress (tensile) due to the bending moment about the x-axis;
3. normal stress (compressive) due to the weight.

What are the stresses at the other points?

Stress State at Pt. A

Step 3. By knowing the loads (forces, torques and moments) that occur at the cross-section, the stresses that act on the other elements can also be found:

Loads Causing Stresses:
Load	Mast Acts as	Stress Equation	Pt. A	Pt. B	Pt. C	Pt. D
Torque, T	Torsion Member about z-axis		Yes	Yes	Yes	Yes
Shear Force, V	Beam about x-axis		No	Yes	No	Yes; opposite stress of torsion
Moment, Mx	Beam about x-axis		Yes (+)	No	Yes (–)	No
Moment, My	Beam about y-axis		No	Yes (–)	No	Yes (+)
Axial Force, W=Ws+Wm(z)	Axial Member		Yes (–)	Yes (–)	Yes(–)	Yes (–)

Notes on Normal Stresses:

• (+) means normal stress is tensile.
• (–) means normal stress is compressive.
• I_x and I_y are the moments of inertia about the x- and y-axes at the centroid of the cross-section, respectively. Due to symmetry they are equal.

Notes on Shear Stresses:

• At Point B, the Shear Stresses ADD as they are in the same direction (+y-direction);
• At Point D, the Shear Stresses SUBTRACT - they are in opposite directions.
• Below, C_s = (4/3)[(R_o² + R_oR_i + R_i²) / (R_o² + R_i²)]