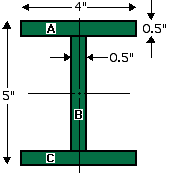
Given: Consider the I-Beam cross-section shown at right.
Req'd: Determine the moment of inertia of the cross-section about the horizontal axis shown (through its centroid).
| Practice Problem 6-1 | Back | Index | Next |
|
Given: Consider the I-Beam cross-section shown at right. Req'd: Determine the moment of inertia of the cross-section about the horizontal axis shown (through its centroid). |

|
For section B - the web - we get:
IB = bh3/12 = (0.5)(4)3/12 = 2.67 in4
For sections A and C - the flanges - since their centroids are each 2.25" above (below) the centroid of the entire cross-section, we use the Parallel Axis Theorem:
IA = IC = bh3/12 + Ad2 = (4)(0.5)3/12 + (4·0.5)(2.25)2 = 10.17 in4
Thus the moment of inertia for the entire area is:
I = IA + IB + IC = 10.17 + 2.67 + 10.17
I = 23.0 in4
The solution can also be obtained using the Shape Calculator Module.
| Top | Back | Index | Next |