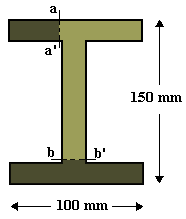
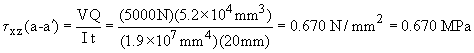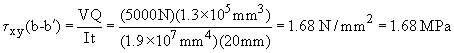Given: A cantilever beam, is built in at the left end, has length L, and rectangular cross-section of width b, and height h. The beam is loaded by point load P at its free end.

Req'd: Determine the shear stress at the top, bottom and neutral axis at a cross-section in the beam.

Sol'n: The shear force, V(x) = P, is constant across the entire beam. At the top (or bottom) surface (y = ±h/2), y^* = h/2 and A^* = 0, therefore t = 0.

At the neutral axis (y₁ = 0), y^* = h/4 and A^* = bh/2. Thus:

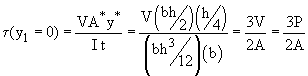
The shear distribution, calculated as a function of y (= y₁), is a parabola, given by the function:

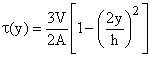
Note that these equations for t(y) are only valid for beams of rectangular cross-section.

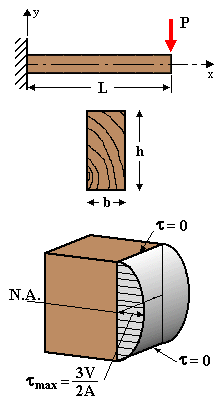
Note: shear-stress acts parallel to the beam-face. The parabola is a plot of the magnitude of the shear stress.

Given: The I-beam at right is subjected to shear force, V = 5 kN. The flange and the web both have a thickness of 20 mm, the height of the beam is 150 mm and the width is 100 mm. The beam has a moment of inertia of I = 19x10⁶ mm⁴.

Req'd: Determine the shear stress at a-a' and b-b'.

Sol'n: The first moment of area (about the neutral axis of the entire cross-section) of the area to the left of a-a' is:

Q = A^*y^* = [(40 mm)(20 mm)](65 mm) = 5.2x10⁴ mm³

y* =[ (150/2 mm) - (20/2 mm)] = (half the height of the cross section) minus (half the thickness of the flange).

Then the shear stress is in the flange is:

The shear stress in the web just above (below) the lower (upper) flange, is:

t^_xy = 1.68 MPa