3c. General Stress and Strain  (SSES Ch. 3.3)
• General Stress • General Strain • Plane Stress • Plane Strain
• Special Cases 		Back | Index | Next
General Stress
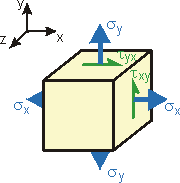
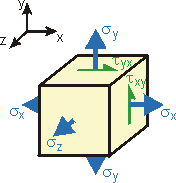
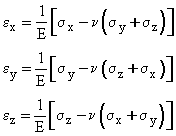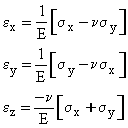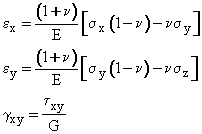Stresses actually vary from point-to-point in a component. A material point can be thought of as an infinitesimal cube aligned in an orthogonal coordinate system (e.g., x-y-z). Each face of the cube has three stresses acting on it:
  • a normal (axial) stress perpendicular to the face,
  • two shear stresses parallel to the face in the other two coordinate directions.

Applying equilibrium, it can be shown that there are only 6 unique stresses needed to describe a state of stress:

(sx ; sy ; sz ; tyz = tzy ; tzx = txz ; txy = tyx )

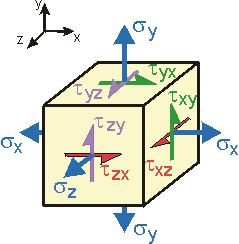
3-dimensional stresses drawn in their positive senses.

  • Stress subscripts refer to (1) the face on which they act, and (2) the direction in which they act. Thus, txy is a shear stress on the x-face acting in the y-direction.
  • Stresses are positive if they physically act on a positive face in a positive direction or act on a negative face in a negative direction (as drawn above).
  • Stresses are negative if they physically act on a positive face in a negative direction or act on a negative face in a positive direction (e.g., a negative sign indicates the stress acts opposite drawn above).
General Strain
For a homogeneous (the same at every point) and isotropic (the same in every direction) material, the normal strain in the x-direction ex is caused by all three normal stresses: sx causes a direct strain, while sy and sz cause transverse strains via the Poisson Effect. The normal strains in the other two directions are calculated in a similar manner:

The shear strains do not exhibit a Poisson-type effect:

In general, all stresses and strains are non-zero.

Plane Stress
Plane stress problems occur where the structure is thin in the out-of-plane direction (e.g., the z-direction) relative to its in-plane dimensions, and there is no resistance to out-of-plane displacement. Thus there is no out-of-plane stress. Any out-of-plane stress is zero:

The non-zero strains are:

Most problems in the text can be considered plane stress problems.

Plane Stress Case.

Plane Strain
On the other extreme are plane strain problems. Here, no deformation is allowed in the z-direction. Any strain with a z-subscript is zero:

= 0

The non-zero strains are then:

Plane strain problems occur when the thickness of a structure in the third (z-) direction is large or comparable to the other two (in-plane) thicknesses, or the z-dimension is otherwise constrained (e.g., kept from expanding by being between rigid supports).
Special Cases (click on description to see illustration)
  • Uniaxial stress: Normal Stress on an element that occurs in only one direction; no Shear Stress.
  • Biaxial stress: Normal Stresses in 2 directions; no Shear Stress.
  • Triaxial stress: Normal Stresses in all 3 directions; no Shear Stress.
  • Hydrostatic stress: Equal Normal Stresses in all 3 directions; no Shear Stress.
  • Pure shear: Only Shear Stresses acting on an element (usually 2D).
Top Back | Index | Next
Updated: 05/24/09 DJD