2.1 Statics Fundamentals
• Vectors and Forces • Free-Body Diagrams • Equilibrium 		Back | Index | Next
Vectors and Forces
A solid grasp of vectors is vital in solving problems in Statics and Strength of Materials. Vectors describe the magnitude and direction of forces and torques/moments. It is often convenient to transform or reduce vectors into their scalar components; e.g., the force at right, F, can be broken into its x and y components:

 Fx = Fcosq   and   Fy = Fsinq 

where F is the magnitude of force F, and q is its direction measured from the x-axis.
Free-Body Diagrams
The construction of free-body diagrams (FBDs) is the first and most important step in solving a Strength of Materials problem. The following steps are involved in constructing a FBD:
  • Clearly isolate from its surroundings the part(s) of the system that you are interested in analyzing; visualize or actually draw a boundary around the body of interest.
  • Identify and represent ALL external forces (and moments) acting on the body - the forces that act across the boundary; include weight when comparable to the applied forces;
  • Include a coordinate system and necessary dimensions on the diagram for convenience in applying equilibrium equations and communicating geometry.
  • The diagram should be free of clutter and extensive information. The forces, moments and key dimensions are the primary information required.
To help illustrate the construction of a FBD, consider the rear suspension of the mountain bike below:

Full Suspension Bicycle

Free-body diagram of rear suspension
Equilibrium
Once a FBD system is constructed, the next step is to apply the concepts and conditions of equilibrium. A body in static equilibrium is not accelerating, so the forces and moments acting on it must sum to zero in any directions. The equations of equilibrium require that the following conditions be satisfied:
  • the sum of the forces in any direction must be zero, and
  • the sum of the moments about any point in a plane must be zero.

In 3D components:

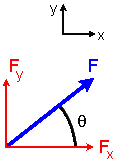
S Fx = 0 ;     S Fy = 0 ;     S Fz = 0

S Mx = 0 ;     S My = 0 ;     S Mz = 0

In 2-dimensions, only three equilibrium equations are required. When the object is in the x-y plane, one of the following three forms may be used:

S Fx = 0
S Fy = 0 
S Mz = 0
S Fx = 0
S Mz,A = 0
S Mz,B = 0
S Mz,A = 0
S Mz,B = 0
S Mz,C = 0
The sum of forces in x and in y, and the sum of moments about any point (about z), equal zero Points A and B are two different points. A, B and C are three points, not all on the same line.

Many problems can be reduced to 2-dimensions.
Top Back | Index | Next
Updated: 02/15/09 DJD