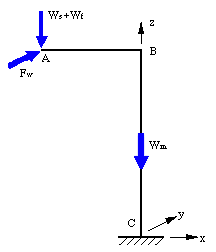
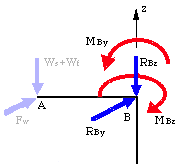
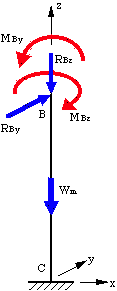
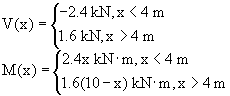Given: In an attempt to pull a nail out of a piece of wood, force P = 20 lb is applied perpendicular to the handle of a hammer. A block is placed under the hammer to provide leverage. The hammer pivots (rocks) at Point A. Let L = 10 in., q = 15o and r = 2.0 in.
Req'd: Determine the tensile force in the nail before the nail begins to slide (the nail remains at rest so had zero acceleration).
Sol'n: Tensile force F can be determined by taking the FBD of the hammer and summing moments about Point A. Taking counterclockwise moments as positive:
SMA = –PL + Fr = 0
F = PL/r = [(20 lb)(10 in.)] / (2.0 in.)
F = 100 lb
Note that angle q is not needed since P is normal to the handle.
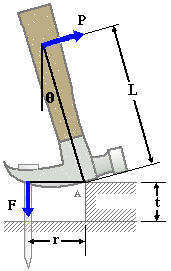
Applied force P and force of nail on hammer. What forces are missing if this is to be a correct FBD?

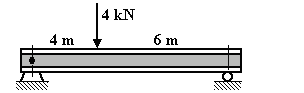
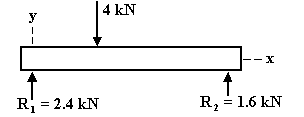
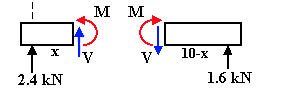
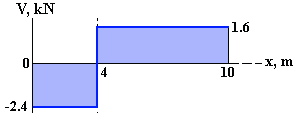
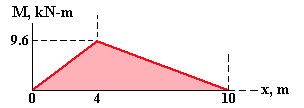
 (4 kN)(6 m) – R1(10 m) = 0
(4 kN)(6 m) – R1(10 m) = 0